
< Uncertainty >
이번 챕터는 자연어처리때 했던 익숙한 몇몇.의 내용들이 보인다. 확률에 관한 지식들을 보충해 가면서 들으면 좋을 것 같다. 확률적인 모델들은 딥러닝이 해결하지 못하는 부분들을 해결하는 경우도 많고, 그 기초가 되기도 한다. 기본적인 내용들에 대해서 다뤄보도록 한다.


기본적인 확률에 대한 표기법과 설명이다. 알다시피 어떤 공간 안에서 특정 event가 일어날 확률을 말하며, 그 확률은 0~1사이의 값중 하나이다. 또한 모든 사건이 일어날 확률을 더하면 1이 된다.

어떤 event들이 확률값들과 Mapping된다는 점에서 function 이라고 볼 수도 있다. random variable이라는 것은 바꿔 말하면 '확률변수'이며, 확률현상에 의해 결과값이 확률적으로 정해지는 변수를 의미한다.

다음은 random variable에 대한 설명이고 세가지 종류가 있다. boolean, discrete, continuous가 그 세가지 이다. true,false가 되거나 몇가지의 값의 보기가 정해저 있는 경우, 값의 범위가 정해져 있는 경우이다.

prior or unconditional probabilities라는 것은, event가 발생할 확률이 얼마가 될 것이라는 정보가 이미 알려져 있는 경우를 뜻한다. probability distribution은 발생가능한 모든 상태에 대한 확률값들을 나열한다. joint probability distribution이란 이 두가지의 경우를 섞어 표기하는 것을 말한다.

Continuous variables의 형태에는 가장 대표적으로 Uniform distribution의 형태가 있다. 어떤 확률이 인터벌의 크기에 비례하다는 것이다. 그림에서 18~26 사이의 크기는 8이므로, 각 포인트에서 어떤 구간의 event가 일어날 확률은 그 면적이 그에 해당하는 값이 된다. 당연하게도, 18~26이라는 event 전체의 확률은 0.125 x 8로 1의 값이 나오는 것을 알 수 있다.


특정한 사건에 대해서만 확률을 계산하는 경우도 있다. 여기서 P(cavity | toothache ) = 0.8 가 무슨 뜻인지 아는것은 중요하다. 이는 절대 toothache가 있다면 그 80% 가 cavity라는 게 아니다. 내가 toothache가 있는 환경에 놓여있는데, cavity일 확률이 0.8이라는 것이다.이 교재에서 Cavity, Toothache와 같이 첫글자가 대문자로 표기되어 있다면 이는 variable, 즉 변수이다. 소문자로 표기되어 있다면 이는 값에 해당한다. 변수의 확률에 영향을 미치지 않는 변수들도 있다. 이런 경우들은 과감하게 없애버릴 수도 있다. 이를 formal하게 나타내보면

위와 같이 나타낼 수 있다. 예전에 확률,통계 수업을 들을배 배웠...던 것 같다. 생각해보면 말을 수식으로 표현한 것 뿐이다 . P( a | b)는 b라는 조건이 선행되어야 한다. 따라서 확률을 계산할 때는, b가 일어날 확률 중에서, a,b가 일어날 확률이라고 생각하면 된다.

Joint Distribution은 다음과 같이 table의 형식으로 나타낼 수 도 있다. 이런 방식을 사용하면 다음과 같은 다양한 조건에서의 확률에 대한 계산이 편리해진다. 테이블에서 한눈에 확인이 가능하기 때문이다. 찾아서 더하기만 하면 게산가능...




이중 마지막 경우에는 Normalization에 관한 얘기가 나온다. 일전에 말했듯이 대문자로 시작하는 단어는 변수를 의미한다. 더불어 이는 참일수도, 거짓일 수도 있다는 말이다. 식 맨 앞에 나오는 알파는 정규화 상수이다. 분모로 나눠지는 부분을 이렇게 처리하기도 한다.

만약 Y에 대한 확률을 구하고 싶은 경우에, 그 경우를 여러 z의 경우로 쪼개어 구한 다음, 이 확률들을 더하는 방법도 있을 수 있다. 여기서 콤마는 &를 뜻한다.

Y는 우리가 관심있는 query variable들이고, evidence로 주어지는 E가 있고, 그 외에 hidden variable들이 있다.

결국 d개의 변수가 각각 n개의 상태로 나눠진다고 하면, 이를 표현하기 위해서는 d^n의 complexity가 필요하다. 따라서 이를 좀 더 슬림하게 만들 필요가 있다. 그 방법은 다음과 같다.

Variable들을 살펴봤을 때, Independent 한 변수들이 있다면, 이를 통해 좀더 필요한 entry들을 줄일 수 있다. 예를 들어 weather는 나머지 cavity, toothache, catch와 관련성이 없는 독립적인 변수이다. 그래서 toothache,cavity,catch는 binary이므로 8개, weather는 아까 4개 의 보기가 있었으므로 그대로 4개. 따라서 총 12개의 entries만 있다면 나타낼 수 있다.

여기서 착안한 아이디어가 conditionally independent이다.

p(cause|effect)는 p(원인|현상)이다. 이 원인이 원인1일 확률, 원인 2를 나타낼 확률을 말한다. 다시 말해, 위의 예제로 보면 목이 결리는 현상이 발생했을 때, 그 원인이 뇌수막염일 확률이 있다. 그런데 이를 직접적으로 조사해서 확률을 그대로 계산하기에는 쉽지 않다. 수많은 목결림 현상중에 뇌수막염을 검색해야 하기 때문이다. 하지만 반대로 뇌수막염중 목결림이 나타낸 경우를 검색하기는 쉽니다. 소규모에서 검색하기 때문이다. 따라서 이런 방법으로 확률계산을 현실적으로 편리하게 진행할 수 있다.

그래서 보통 마주치는 문제들은 바로 다음과 같다. 이런저런 effect가 나타났을 때, 그 원인이 무엇인지를 알아내야 하는 것이다. 따라서 우리는 bayes' rule과 conditional independence를 이용해서 문제를 간결화시킨다. 이런 방식으로 하면 문제가 굉장히 간결해지는 장점이 있다.

Wumpus world에 대해서 알아보자. pit는 구덩이 이다. 목적은 구덩이를 피하는 것인데, 이 pit이라는게 어디에 있는지 모른다. 이중에서 구덩이가 있을 확률은 0.2이다. b는 breezy 상태라는 건데 바람이 들어온다는 것은 붙어있는 square중에 pit이 있다는 것이다. 이 상황에서 어디가 pit인지는 모르는 상황이므로 (1,3), (2,2), (3,1)중에서 pit이 없을 확률이 제일 높은 것으로 가야 한다.

그러면 이 문제를 어떻게 해결할 것인지 생각해 보자. 각 square에 대한 random-variable이 있고, breeze의 여부는 3개의 블럭만 알고 있다. breeze라는 것은 어떻게 보면 현상이라고 볼 수 있다. 그 값은 0|1이 된다. 그 이후의 값들은 각 square에 대한 확률로 binary값은 아니다. 각각의 value는 independent 하므로 수식으로 나타낼 수 있다.

문제에서 우리가 알고 있는 팩트값에 대해 알아보자. 일단 b11은 f, b12와 b21은 t이다. 거기에 더해서, p11,12,21은 breeze이므로 pit이 아니라는 사실을 알 수 있다. 이 6가지 정보를 가지고, 노란색 지점에서 pit의 확률을 알아보자. unknown을 p13과 b들을 제외한 부분으로 정의하도록 하자. 그러면 나머지 것들에 대한 p13의 확률은 위의 수식과 같이 정의된다.
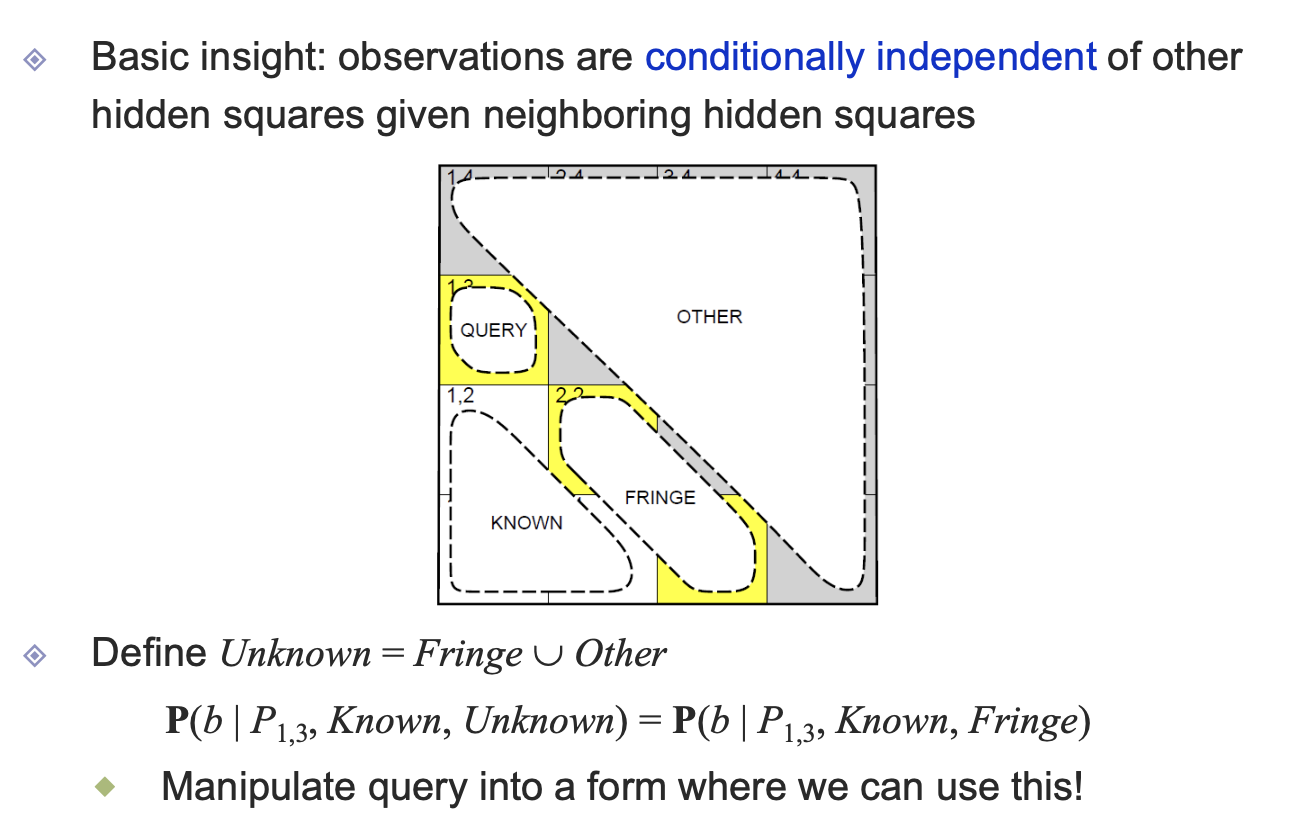
unknown 은 other과 fringe부분이다. known하고는 conditional indepence하다고 말할 수 있다. 따라서 other이라는 부분은 생략해도 무방하다.

그래서 수식을 따라가게 되면 위와 같다. b와 known을 알고있고, p13을 구하고 싶다. 이를 위해서 marginalization을 진행하면 이어서 나오는 모습과 같이 된다. 그 후 unknown부분을 fringe부분과 other 부분으로 나누었다. 이때 independence에 대한 값을 상수처리해서 앞으로 옮긴다. 계속해서 상수화 시킬수 있는 부분들을 추가하면 위와 같이 간략화 할 수 있다.

이 확률을 이제 실질적으로 구해보도록 하자. pit일 확률은 <true:02. false:0.8>이다. 그리고 fringer각각에 대해서 값을 구해야 한다. fringe에는 square22,31이 있다. square가 true일 경우에, fringe에서 두개 다 pit일 경우, 하나는 pit고 하나는 pit이 아닐 경우. 둘다 pit이 없을 확률인데, 만약 둘다 pit이 없다면- 2,1이 b가 될 수 없다. 따라서 둘다 아닌 경우를 제외하면, <0.2, 0.8><0.04+0.16+0.16+0, 0.04+0.16+0+0>이므로 계산하면 <0.31,0.69>가 나온다. 여기서 알파프라임 값은 true와 false에 대한 확률의 합이 1이 나오도록 계산하면 되기 때문에 처음부터 생각할 필요는 없다.
'[ML] > [Lecture]' 카테고리의 다른 글
| [ML/Lecture] 5. Inference in BN (0) | 2020.06.20 |
|---|---|
| [ML/Lecture] 4. Bayesian Networks (0) | 2020.06.20 |
| [ML/Lecture] Assignment #1. solving N-Queens (using genetic -algorithm) report. (0) | 2020.05.03 |
| [ML/Lecture] 2. Informed Search Exploration (0) | 2020.04.08 |
| [ML/Lecture] 1. Solving Problems by Searching (0) | 2020.04.02 |




