
< Bayesian Networks >



베이지안 네트워크의 간단한 예시를 보여주고 있다. 내용은 간단하다. 도둑이 들면 알람이 울리고, 지진이 일어나도 알람이 울린다. 알림이 울리면 john과 marry가 각각 이를 인식해서 알려준다는 네트워크이다. 이를 확률과 함께 나타내면 아래 그림과 같다.

도둑이 들 확률은 0.001이다. 지진이 일어날 확률은 0.002이다. 도둑이 들고, 지진이 일어났을 경우에 알람은 0.95의 확률로 울린다. 반대로 도둑도 들지않고, 지진도 없는데 알람이 실수로 울릴 확률은 0,001에 불과하다. 또한 알람이 울렸을 경우에, john이 나에게 알려줄 확률은 0.9이고, 알람이 안울렸는데도 나에게 알려줄 확률은 0.05이다. 이런 방식으로 네트워크를 작성해 놓으면 각 사건이 일어날 확률이 얼마나 될 것인지 파악할 수 있다.

CPT라 함은 conditional probability table을 의미하는데 부모노드가 k개가 있다면, 2^k의 row가 있다고 할 수 있다. 마찬가지로 아닐 확률은 1에서 빼면 된다. 위의 그림에서 B,E,A,J,M은 각각 1,1,4,2,2의 number가 필요하다. b,e는 true/false를 나타내는 변수 한개씩만 있어도 되지만, a는 b,e가 true/false임에 따라 총 4개의 변수가 있어야한다.

파란색 상자를 보면 chain-rule로 전개한 식이 나와있는데, 불필요한 조건들을 제거할 수 있음을 보여주고 있다. 즉, parent-node의 조건이 주어진다고 하면 independent하므로 그냥 곱하기만 하면 되는 것이다. 즉, j이고 m이고 a인데 b도 아니고, e도 아닌 확률을 계산한다고 하면 위의 그래프에서 다음과 같이 계산하면 되는 것이다. 먼저 알람이 울릴때 j의 확률, m의 확률을 곱하고, 알람이 울릴 확률(b도 아니고 e도 아닌 상황에서), 마지막으로 b도 아니고 e도 아닌 확률을 곱해야 되는 것이다.

결국 베이지안 네트워크를 구성하는 것은 chain-rule에 따라 다음과 같이 이루어 지는 것이다.

결과적으로 본다고 하면, 이루어지는 과정은 다음과 같다. m,j,a,b,e의 순서로 ordering이 이루어졌다고 가정해보자. 그러면 m일때 j의 확률과, j의 확률을 본다. 만약 다르다고 하면 독립적인 관계가 아닌 것이다. 따라서 우선순위에 따라 m의 true/false여부가 j에 영향을 미치므로 화살표을 그어준다. 아래도 마찬가지이다. m이 a에 영향을 미치므로 m에서 a로도 그어준다. 또한 j,m이 a에도 영향을 미치므로 j에서 a로도 그어준다. 세번째 줄에서는 j,m이 b|a에 영향을 주지 않으므로, 직접 선을 연결하지는 않지만 4번째 라인을 보면 a는 b에 영향을 주기때문에 a에서 b로는 선을 그어준다. 마찬가지 작업을 반복하면 된다. 마지막 두줄로, b,a,j,m중에서 a,b만 영향을 미친다고 생각하면 된다.

다음 상황만 봐도 알겠지만, 같은 m,j,a,b,e가 일어날 확률을 구하지만 order에 따라 필요한 number에는 차이가 날 수 있다. 위의 경우는 13개의 variable이 필요하지만, 아래의 경우는 10개만 있어도 가능하다.

다른 방법으로는 위 그림과 같이 hidden variable들을 사용하는 방법도 있다. hidden variable이 없는 경우에 각 노드들을 연결시키는데 훨씬 많은 parameter들이 필요하지만, hidden variable로 이를 묶어주게 되면 파라미터들이 2^n으로 늘어나게 되는 케이스들을 줄여줄 수 있다.

또 다른 관계로 위와 같은 경우가 있을 수 있다. parent condition인 a가 주어졌을 경우에, non-descendent한 c는 conditionaly independent하게 된다.

이와 관련된 내용으로 markov blanket이라는 것이 있다. markov blanket이란 위의 그림에서 보이는 것 처럼 부모노드, 자식노드, 자식의 또다른 부모노드를 일컫는 용어이다.
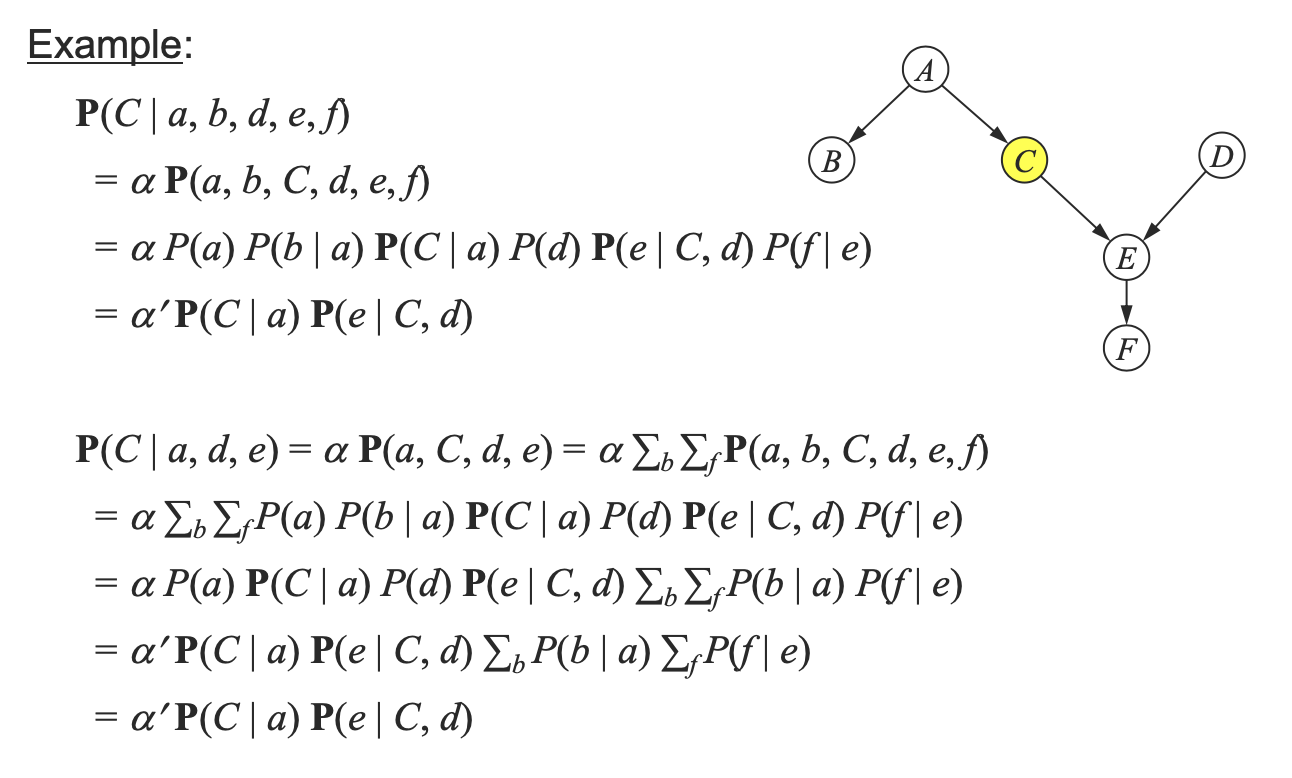
다음 예제에서 노드 c의 markov blanket은 a, e, d라고 할 수 있다. 위의 예제와 아래의 예제를 보면 알 수 있듯이, 해당 노드에 대해 markov-blanket을 포함하고 있다면, 추가적인 조건들이 덧붙여진다고 하더라도 확률은 같다는 것을 알 수 있다.

continuous한 value의 cpt는 사실 무한대로 그 크기가 커질 수 있다. 따라서 discrete한 형태로 데이터를 구간별로 짤라 사용하는 것이 한가지 방안이 될 수 있다.
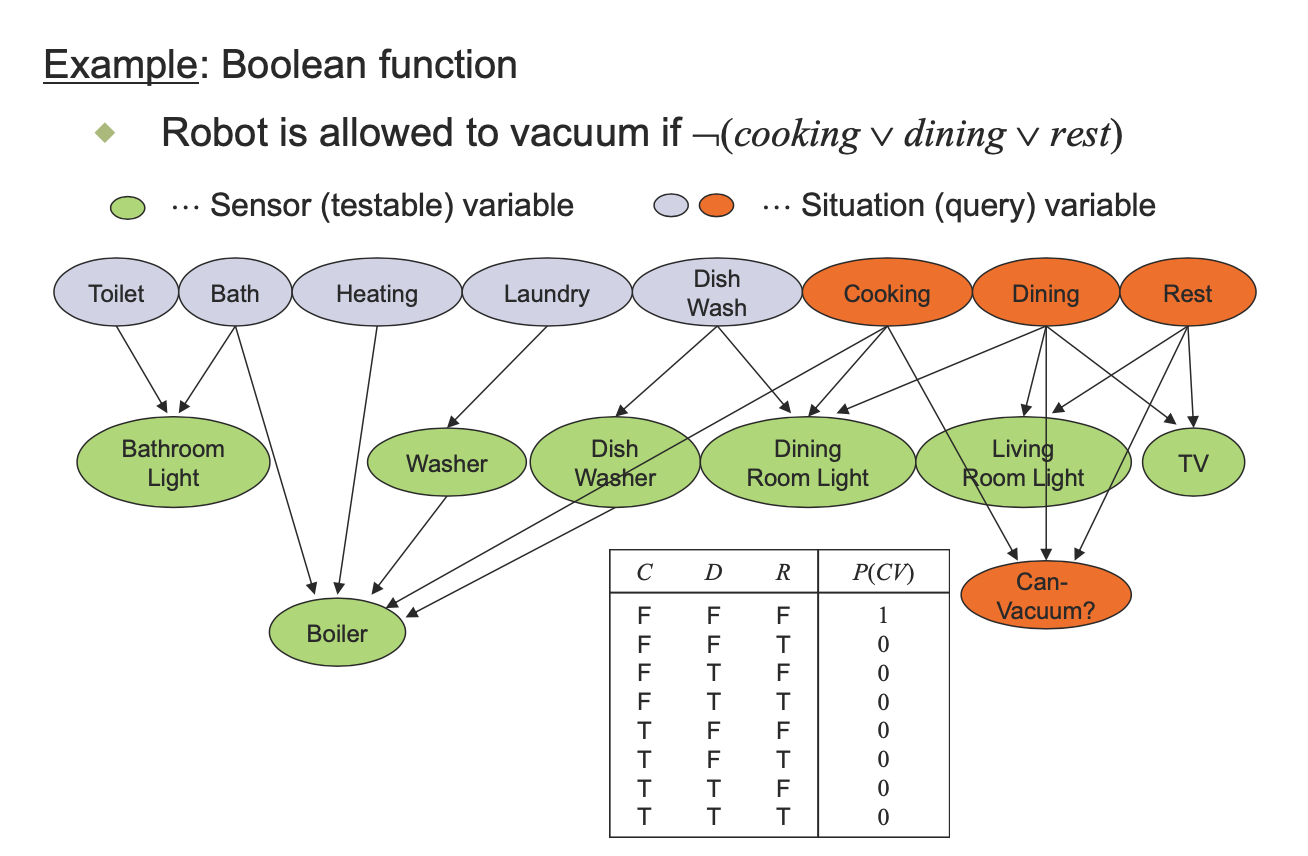
다음과 같은 예제를 보더라도 C,D,R이 모두 F인지 아닌지만 확인하면 되기 때문에 매우 compact해지게 된다.

C,F,M변수에 따라 fever의 negation을 보면 마치 independant한 관계처럼 계산할 수 있고, 1에서 뺴면 Fever의 발생확률을 알 수 있다.

하이브리드 네트워크는 discrete한 노드와 continuous한 노드의 input이 들어올 때 어떻게 해결하겠느냐는 질문인데, 여러가지 방법이 있다. 먼저 continous한 value를 discretization할수 있다. 이렇게 되면 네트워크는 만들어지지만 구간수도 늘려야 하고, boundary를 기준으로 value를 나누면 오차가 들어가므로 오류가 발생할 확률이 높아진다.

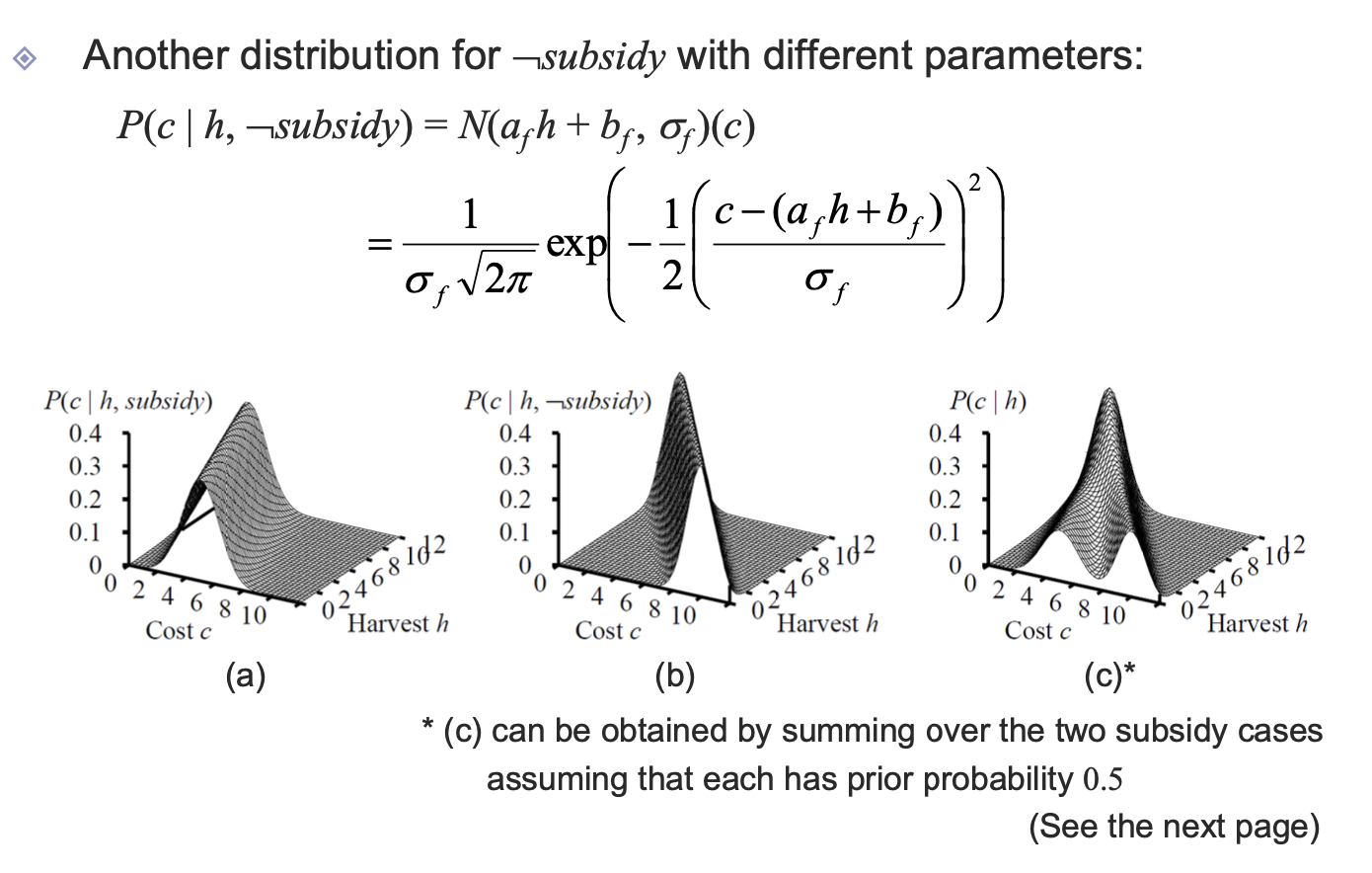

결국 continous한 child variable의 경우에는 discrete에 해당하는 subsidy가 true인지 false인지에 따라 나우어 계산하고, 그 각각의 모델의 합을 통해 전체적인 모델을 얻어내게 된다.

그렇다면 child node가 discrete하고, parent node가 continous한 경우에는 어떻게 할까? 아마 일정수준의 경계값을 정하게 될 것이다. 그래야 discrete하게 결론지을수 있기 때문이다. 이때 사용하는 것이 다음과 같은 probit distribution이다.

probit distribution을 사용하게되면 결론적으로 true/false로 output을 내게 된다.

logistic function(혹은 sigmoid)를 사용하기도 한다. 위의 그래프에서 볼 수 있듯이 logic과 probit distribution의 값이 거의 비슷한 것을 알 수 있다. sigmoid가 tail이 조금 더 길기는 하다고 한다. 실제 모델을 만들면서 activation function으로 많이 쓰는 sigmoid가 바로 이것이다.
'[ML] > [Lecture]' 카테고리의 다른 글
| [ML/Lecture] 6. Learning from Examples (Part A) (0) | 2020.06.25 |
|---|---|
| [ML/Lecture] 5. Inference in BN (0) | 2020.06.20 |
| [ML/Lecture] 3. Uncertainty (0) | 2020.05.04 |
| [ML/Lecture] Assignment #1. solving N-Queens (using genetic -algorithm) report. (0) | 2020.05.03 |
| [ML/Lecture] 2. Informed Search Exploration (0) | 2020.04.08 |




