
< Informed Search Exploration >
이전까진 uninformed-search에 다뤘었다. 하지만 정보를 좀 더 사용하면 효율적인 탐색이 가능하지 않을까?
informed search에 대해 알아보자. 알아볼 내용은 다음과 같다.


먼저 Informed Search Strategy이다. 이전까지는 node들이 다 같은 value를 가지고 있었다면, 이번에는 evaluation function으로 노드의 탐색할 순서를 정하게 된다. 이때 evaluation func은 위의 슬라이드에서 보이는 것처럼 g(n)과 h(n)으로 나뉘어져있다. 이전에 예제로 사용했던 도시 탐색 그래프를 떠올려 보자.

그래프를 보면 기존에 사용했던 path-cost 이외에도 heuristic function이 추가되어 있는 것을 볼 수 있다. 이 경우에, heuristic function을, 각 도시에서 도착도시까지의 physical-distance, 직선거리로 정의했다. heauristic funtion이라는 것은 직관적으로 예측하는 함수이며 오차가 존재한다. 즉, optimal이 보장되지는 않는다.

다시 evaluation function으로 돌아가보자. f(n) =g(n) + h(n)이라고 정의되어 있다. 이때 g(n)은 path-cost, h(n)은 distance이다. 이 evaluation function에 path-cost(g(n))만 남기는 방법이 uniform-cost search였다. 새롭게 정의한 physical distance에 해당하는 heuristic function을 evaluation function으로 사용하는 것이 greedy search이다. 다음 예시를 보면서 확인해보자.

결과를 보면 알겠지만 goal-state에 도달하는 경로는 solution이지만 optimal하지는 않다. 평가는 다음과 같다.

보면 finite한 space에서도 loop에 빠질 위험성이 존재한다. 이를 방지하는 방법은 다음과 같다.

결국 각각의 uniform-cost와 greedy를 보완하기 위해서는 두가지를 합치는 방법이 있다. 이를 A* search라 한다.

g(n)을 현재지점까지 오는데 필요한 cost라 하고, 선택하는 과정은 다음과 같다.
(tree-search)

(graph-search)
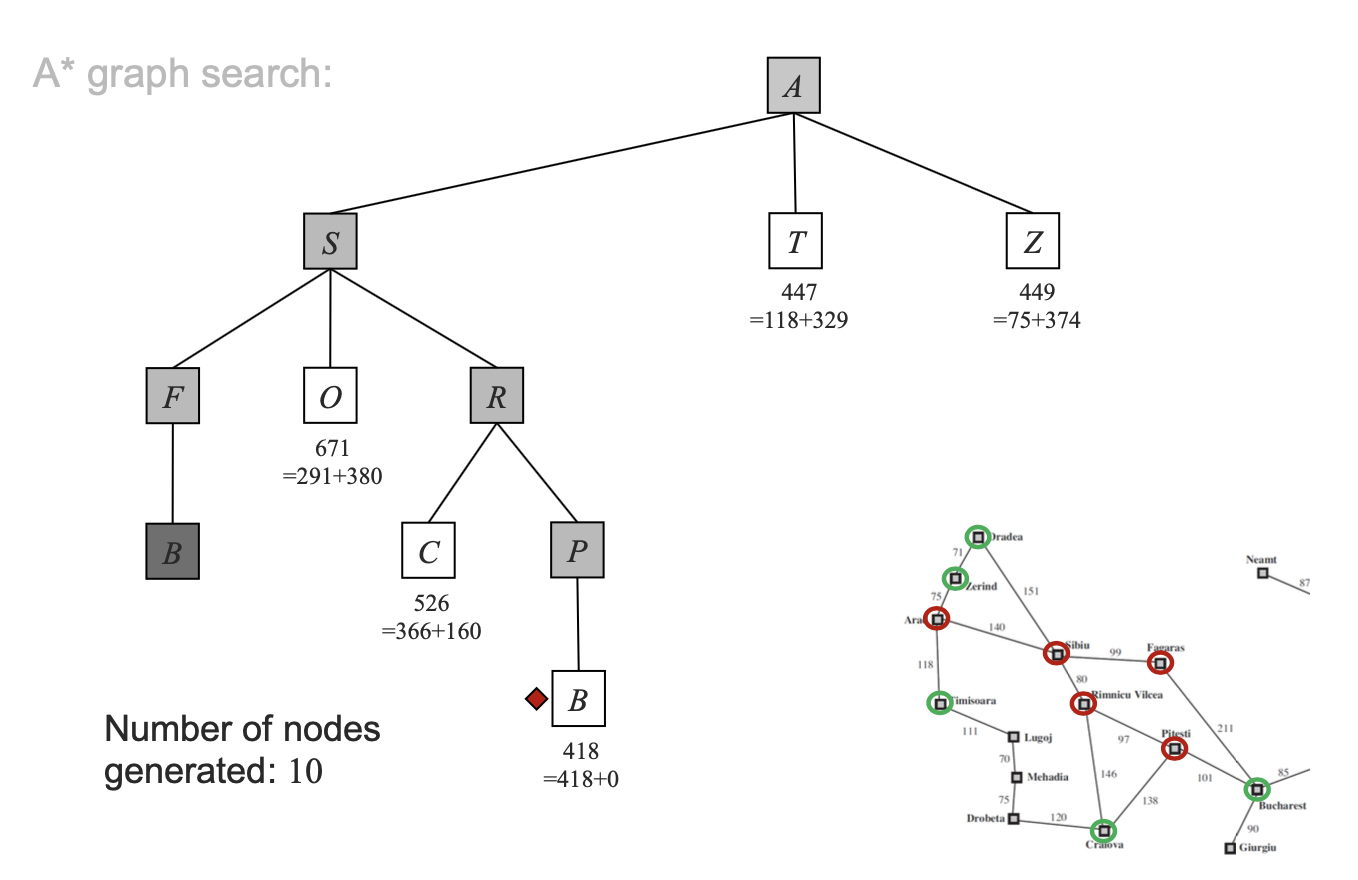
그럼 지금까지의 내용을 한번 정리해보도록 하자.

Tree에서 A* Search는 Solution은 찾는 것 처럼 보인다. 문제는 이 search가 optimal인지 아닌지를 보는 것이다. 그리고 그 핵심은 heuristic function인 h(n)이 어떤 값을 가지게 되느냐이다. 증명을 위해 C*가 optimal cost라고 정의하자. 그리고 frontier list에 G2라는 goal-node가 있다고 생각해보자. 그러면 f(G2)는 G2 노드까지의 cost와 , heuristic 값의 합이다. 또한 g2는 suboptimal이므로 optimal한 경우는 아니지만, goal-node이기는 하다. 이때 heuristic값은 goal-node에 도착했으므로 0이 된다. 하지만 f(G2)는 C*보다 크다. 하지만 같은 frontier에 optimal로가는 노드 n이 있다면, f(n)은 적어도 C*보다 작거나 같을 것이다. 따라서 A*알고리즘은 당장에 goal-node인 G2로 가지 않고, 좀 더 optimal한 경우에 해당하는 n노드를 선택하게 되는 것이다. 내가 볼때는 이 부분이 A* search의 핵심이 아닐까 싶다.

다음 경우는 A* Search의 graph에 관한 이야기이다. A* Search에서의 heuristic function은 좀 더 요구하는 요건이 많다. consistency라고 하는데, 다음단계까지의 cost와, 다음단계에서 goal-node까지의 heuristic function값보다 현재노드에서 goal node까지의 heuristic function값이 작아야 한다는 것이다. 이를 만족하지 않는다면 n'으로 가서 goal node로 가는 편이 오히려 optimal에 더 가까울 것이다.

tree A* Search와 마찬가지로, graph A* Search도 증명해보도록 하자. h(n)이 consistent라는 것은 다음노드에서 가는 경로보다, 지금 노드가 더 optimal하다는 것이다. f(n)은 감소하지 않는 함수이다. 따라서 어떤 frontier node인 n'에서 확장하더라도 nondecreasing을 유지하는 경우에만 확장을 한다. 따라서 이후 path에 있는 어떤 goal-node를 선택하더라도 첫 goal-node 확장보다 적어도 비싸질 것이다.

결국 A* search를 정리하자면 다음과 같다. optimal하고 complete하며, time&memory complexity는 exponential이다. 또한 A*는 모든 주어진 heuristic에 대해 optimally efficient이다. 이 말은 f(n)이 C*보다 커진다면, 그 이후는 어짜피 계속 값이 커질 것이기 때문에 그 순간에 바로 잘라내서, 효과적인 탐색이 가능하다는 것이다.

아주 제한적인 의미로 생각해 보면, uniform cost search, breadth-first search, greedy best-first search도 A* Search에 포함된다고 할 수 있다. 그렇다고 A* search로서의 의미를 가진다고 말하기는 힘들다.

사실 모든 문제가 지금까지 배운 것 처럼 path로 나타낼 수 있는 것은 아니다. 많은 최적화 문제에서 path라는 것은 관련이 없기 때문에 상태를 중심으로 맞춰가는 것을 local search algorithms라고 한다. 현재의 configuration을 평가하는 함수로, 지금이 얼마나 괜찮은 지를 알아보는 것이다. 예를 들어 time-table을 만드는 문제나, n-queens problem이 그 예시가 될 수 있다.



현재 state-space에서 global maximum을 찾고자 하는 것이다. local search는 지금의 configuration보다 조금 더 좋은 방향으로 나아가는 것이 목적이다. configuration은 objective funciton(cost-function)으로 판단한다.

Next-State는 어디서 어디로 갈 것인지가 문제의 핵심이다. 출발은 랜덤한 initial한 포인트에서 시작한다. 만약 현재 state에서 successor의 value가 가장 높은 상태로 다음 transition을 정하는 것이다. 다음 포스팅으로 올린 genetic algorithm을 보면 굉장히 유사한 방법으로 next-state를 정하는 것을 알 수 있다.

예를 들어 8-queens problem에서는 각 퀸마다 충돌횟수가 얼마나 발생하는 지를 따져서 그 횟수가 가장 적은 방향으로 next-state를 정하는 방법이 있을 수 있다. 이런 식으로 현재의 상태를 판단해서 좀 더 나은 상태를 찾아가는 것이다.

이는 많은 경우에, local minimun 혹은 local maximum에 빠질 가능성이 있다. 이를 해결하는 방법으로 세가지 정도가 있다.
- 먼저 stochastic hill climbing은 매번 제일 가파른 곳으로 간다고 꼭 좋은것이 아닐 수도 있다. 가파른 곳이 작은 봉우리 일 수도 있기 때문이다. 따라서 그런쪽으로 가지 않도록 매번 제일 가파른 쪽으로 가는게 아니라, 올라가기만 하면 그 곳으로 가보는 것이다. 이런식으로 하면, 결과는 늦게 나오지만, global-maximun을 찾을 확률이 높아진다.
- 두번째는 first-choice hill climbing인데, 이는 랜덤하게 찍은곳이 현재 상태보다 낫다면 successor를 생성하는 것이다. 이 방법은 다른 방법들 보다 빠르다. 다음 state로 가기 위한 evaluation을 일일이 다 해야하지만, 이 방법은 그렇지 않다. 실질적으로 결정은 빨리하지만, global-maximum을 정확하게 빨리 찾는 것은 아니다.
- 세번째는 random-restart hill climbing이다. 이는 시작을 여러번 해보는 것이다. 한번 해서 끝이 아니라, 하나의 봉우리를 찾고 나면, random하게 다음 시작점을 찾고 나서 다시 올라가 보는 것이다. 이를 반복해서 global-maximum을 찾아보는 것이다.

이 방법은 local-maximum에 빠지는 경우가 굉장히 많다. 다른 local-search- algorithm을 알아보자.

Simulated Annealing Search는 중간중간에 튀는 지점을 마련한다는 점에서 특이하다. 여기서 튄다는 것은 겉보기에는 "bad moves"에 속한다. global-minimum을 탐색하는 와중에, 항상 값이 하락하는 방향으로 움직여야 하지만 가끔씩은 값이 증가하는 방향으로 움직이는 것도 허용하는 것이다. 또한 처음에는 "bad moves"를 많이 허용해 주지만 가면 갈수록 global에 근접했다고 판단하고 이를 덜 허용하게 된다. 위에 p(x)의 식에 따라, 온도 T가 낮아질 수록, p(x)라는 "bad moves"가 일어날 확률이 줄어든다. 그렇다면 sudo-code를 확인해 보자.

minimize를 하기 위한 알고리즘이다. 처음에는 random하게 선택을 한다. 그 다음, 만약에 다음 value가 current value보다 낮아진다고 하면 update해버린다. 이는 hill-climbing중에 first-choice hill climbing이랑 비슷하다. 하지만 차이점은 확률이 달라진다는 것이다. 즉, next value가 낮아지는 경우에 대한 확률을 주는 것이다. 비록 T의 값이 회를 거듭할 수록 bad move를 허용하지 않는 방향으로 흐른다.

정리하면 위와 같다. best move보다는 random move를 선택한다. 만약 상황을 더 좋게 만든다면, 이는 항상 수용된다. 하지만 아닌 경우에는 probility 함수에 따라, 발생가능한 확률을 낮춰간다. 만약 이 T가 0이 된다면, 확률도 0이 되기 때문에, 이는 bad moves를 허용하지 않는 first-choice hill climbing과 같다.

Genetic algorithms에 대해서는 assignment posting에서 n-queens problem solving을 통해 자세하게 다룰 것이기 때문에 생략하도록 한다. 요약하자면 아래와 같이 chromosome desiogn에서부터 generation update를 반복하며 fitness function을 통해 최적의 해를 찾아나가는 과정이라고 생각해면 된다.

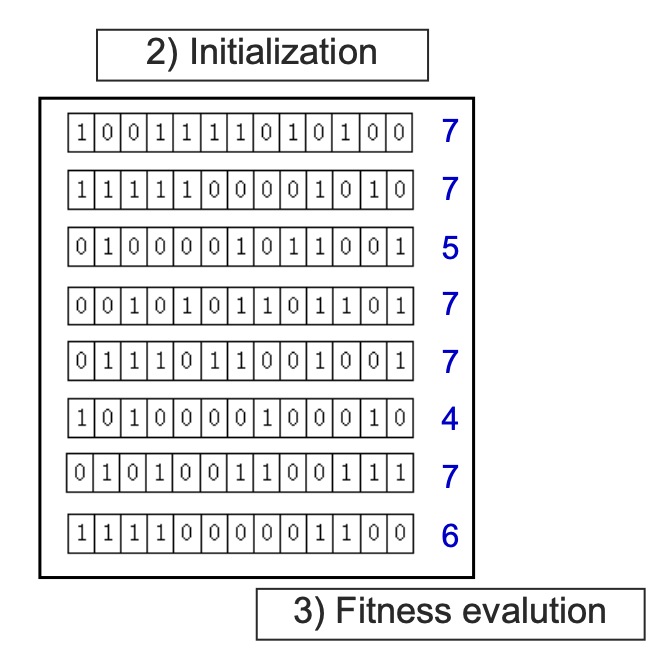


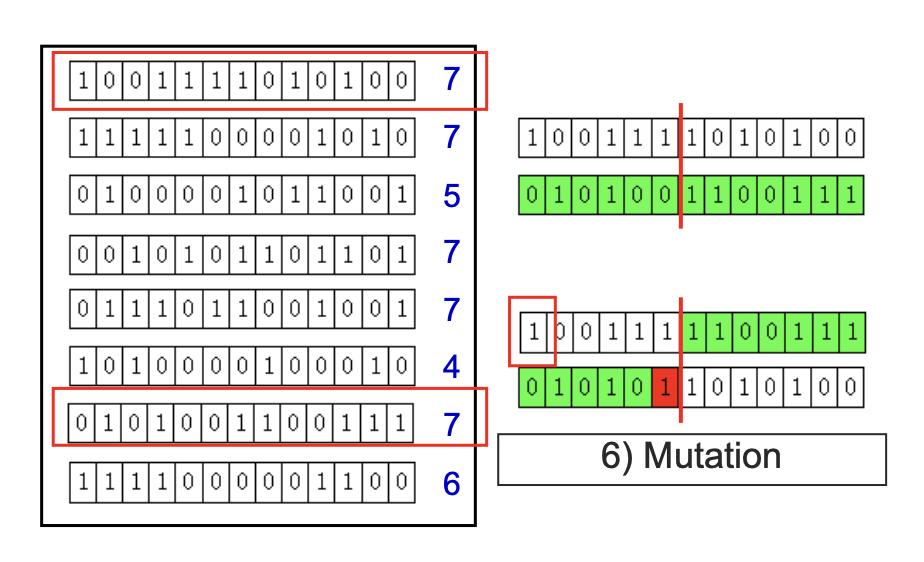

[ 전체적인 genetic algorithm에 대한 요약 ]

'[ML] > [Lecture]' 카테고리의 다른 글
| [ML/Lecture] 4. Bayesian Networks (0) | 2020.06.20 |
|---|---|
| [ML/Lecture] 3. Uncertainty (0) | 2020.05.04 |
| [ML/Lecture] Assignment #1. solving N-Queens (using genetic -algorithm) report. (0) | 2020.05.03 |
| [ML/Lecture] 1. Solving Problems by Searching (0) | 2020.04.02 |
| [ML/Lecture] Intro... (0) | 2020.03.30 |




