
< Solving Problems by Searching >
Problem Solving은 무엇을 의미할까.
ML에서 문제를 해결한다는 것은 초기 상태(initial-state)에서
목적지인 goal-state까지의 'sequence of operators path'를 찾는 것으로 정의된다.


위에 예시로 나온 문제는 유명한 'Traveling Salesperson Problem이다. 각각의 노드를 전부 순회하는 방법을 구하는 문제인데 동일한 노드를 중복해서 지나지는 않는다. 첫번째 방법처럼 combinatorial explosion이 일어나는 경우는 각각의 노드를 중심으로 남은 모든 노드를 순회하는 경우의 수를 모두 따져보는 것이다. 이는 time-complexity를 계산해보면 O(n!)이 나온다. 물론 가능한 모든 경우를 다 따져보기 때문에 확실한 minimun-cost path가 나오지만 이는 효율적이지 못하다. 따라서 좀더 직관적인 효율적인 방법으로 (heuristic한 방법) 각 노드에서 가장 짧은 노드를 찾는 방법이다. 각 노드에서 나머지 노드 중 가장 짧은 노드를 탐색하고, 이 경로를 잇기 때문에 n-1번의 검색을 n-1번 반복하게 된다. O(n^2)이다.( 중복을 허용하지 않는다면 (n-1)*(n-2)* ~~~ * (2)*(1)이 될 것이다. ) 팩토리얼에 비해 유의미한 감소이지만 여전히 minimun은 아니다. NN(Nearest Neighbor) solution의 실패 사례가 나타나있다.

특정 문제를 어떻게 formalize할 것인지도 중요한 문제이다. 이를 위해서, 우리는 initial state, operator를 특정지어야 하며, 이는 state-space(상대공간)를 구성한다. 또한 goal test를 설정하는데 여기서 goal test란 state가 goal state에 도달하였는지를 확인하는 단계이다. 다음은 path-cost function이다. path(solution으로 볼 수도 있다)를 구성하는 각각의 action들의 비용의 합산도 고려해야 할 사항들 중에 하나이다. 우리는 많은 solution(path)중에서 optimal한 솔루션을 찾는다.

Solution을 찾는다는 것은 다양한( 가능한 ) action sequences를 찾는 것이다. 그 방법중에 하나로, 문제를 tree형식으로 풀어낼 수 있다. (data-structure에 나오는 그 tree가 맞다) tree에서 leaf nodes에 해당하는 아직 탐색하지 않는 노드들을 frontier( open list )라 한다. tree-search를 의사코드로 작성한 내용을 살펴보자.

loop do 아래를 보자. frontier가 비어있다는 것은 가능한 모든 곳을 다 탐색했지만 goal state를 찾지 못했으므로 failure를 리턴한다. leaf-node(frontier)를 방문했다면 그 노드는 frontier에서 삭제한다. 탐색 도중 goal state를 찾아낸다면 당연히 성공이다. 이중에서 어떤 leaf-node를 방문할 것인지는 search strategy에 달려있다.

반복된 state들은 어떻게 처리할까? 반복된 state는 loopy path에 의해 생기는데 loopy path는 무한루프를 야기할 가능성이 있다. 따라서 이런 불필요한 path는 걸러낼 필요가 있으므로 이를 따로 저장하는 explored set을 만들기로 하였다. 이는 closed list라고도 하는데, 이곳에 저장된 노드들은 노드를 방문할때 살펴봐서 이미 방문한 노드라고 판별되면 frontier set에서 제거해 재방문을 막는다. 이런식으로 explored set을 유지하는 것을 graph-search algorithm이라고 한다.(tree-search는 explored set이 없다) 이것은 하나의 search strategy이다. 다음은 graph-search의 의사코드이다.

tree-search의 의사코드와 거의 동일하지만, explored set을 초기화 해주고, explored set에 노드를 추가하고, frontier나 explored set이 아닌 노드로만 확장한다는 것이 차이로 드러나있다. 여기서 explored set에 포함되어 있는지를 빠르고 효율적으로 탐색하기 위해 hash table에 넣고 확인하기도 한다. 그렇다면 성능을 측정하기 위헤 고려해야 할 사항들은 어떤 것들이 있을까?

먼저 completeness이다. 어떤 문제에서 solution을 찾을 수 있다면, 우리는 그. 문제가 complete하다고 한다. solution을 찾는다고 보장할수 있는지를 고려해야 한다. 다음은 optimality이다. 이전에 NN전략처럼 효율적이지만, minimum cost를 보장하지 않는 전략도 있었다. 얼마나 optimal한 solution을 내뱉는지도 고려해야 할 사항이다. time complexity, space complexity 또한 당연하게 고려조건이다.

그 다음은 사용되는 기호들인데 b는 branching factor로 분기되는 최대 노드들을 말한다. d는 shallowest goal node의 깊이이고, m은 상태공간에서 최대 path 길이를 뜻한다.

search-strategy에는 정보가 주어지지 않는 uninformed search(blind search)와 정보가 주어지는 informed search(heuristic search)가 있다. 여기서 정보라는 것은 어떤 상태가 goal state로 가는 길에 유리한지에 대한 정보가 주어짐을 의미한다. 지금부터 Uninformed Search Strategies에 대해 알아보자.

처음은 BFS이다. frontier에서 가장 얕고, 확장되지 않은 노드를 먼저 간다. 위의 그래프 처럼 frontier에 해당하는 FIFO queue는 차례대로, [A] -> [B,C] -> [C,D,E] ->[D,E,F,G]로 변화하게 된다. 의사코드를 한번 살펴보자.

먼저 BFS도 uninformed search이므로, path cost는 0이다. graph search이므로 frontier가 비면 failure를 리턴하고, explored set이 존재한다. goal-state인것이 확인되면 solution을 리턴한다. 방문하는 노드는 frontier에서 하나씩 빼서 결정한다. 각 노드에 방문하는 경우마다 child node(func)로 child 를 정하는데, 그 child node가 탐색했던 곳이 아니거나 frontier에 없다면 goal test를 수행해 참인경우 solution으로 리턴한다. BFS 전략을 평가해보자.

BFS는 먼저 complete하고 optimal하다. complete하다는 것은 solution이 존재한다는 것이다. 각 노드들 중에서 goal state가 나올때까지 탐색하니 당연하다. 또한 path cost가 동일하므로(uninformed search이므로) optimal한 solution일 것이다. complexity를 계산할때 worst-case를 따지는 big-O notation으로, 최악의 경우는 각각의 노드의 branching factor가 깊이 d만큼 분기되었을때 나오는 모든 노드들 다 검색하는 것이므로(최하단 leaf node 맨 마지막에 goal state가 존재하는 경우) O(b^d)가 된다. 이럴 경우 깊이가 늘어남에 따라 BFS를 사용하면 필요한 explored set memory역시 기하급수적으로 늘어나는 단점이 있다. 즉, 확실하지만 메모리 비용과 탐색시간이 많이 든다. 따라서 blind search(uninformed)는 exponetial problems에 사용하기가 힘들다. 그렇다면 frontier에서 BFS처럼 shallowest node가 아니라, leash-cost node를 탐색하면 어떨까? 이것이 Uniform-cost search이다.

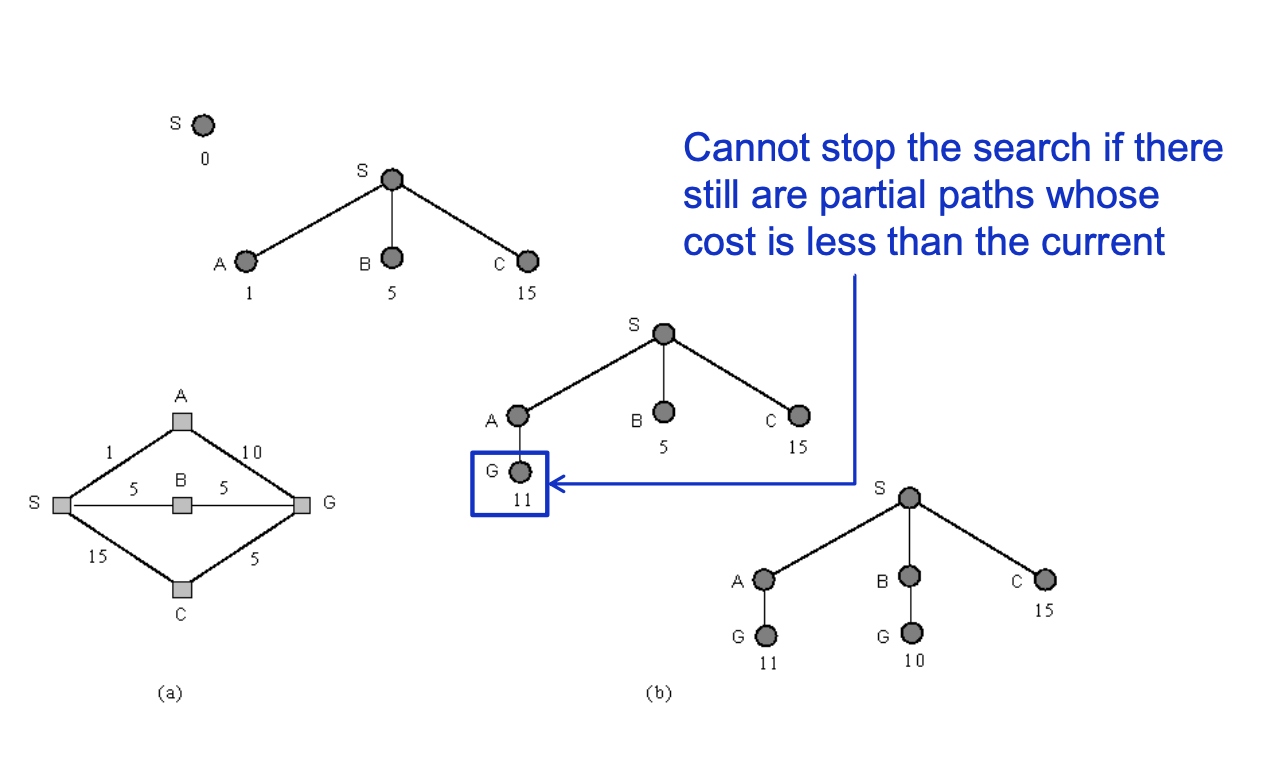
위 그림을 보면 uniform-cost search로 분기해나가는 과정을 보여주고 있다. 그림(a)가 탐색 대상 그래프이다. 시작점을 S라고 할 때, 처음에 S에서 세가지 노드로 분기해 나가는데, cost가 각각 1,5,15이다. 즉 frontier는 [A,B,C]이다. 다음은 노드 A에서 분기를 하고, frontier는 [B,C,G]가 된다. 다음 frontier는 [G,C]이다. G가 10인데, C는 15이므로 더 볼 필요도 없이 G가 solution이다. 의사코드를 한번 살펴보자.

frontier는 path-cost에 따라 prority queue를 만들어 사용한다. goal-test를 시행해서 true로 판정되면 solution을 리턴한다. 만약에 자식노드가 frontier에 들어있고, path-cost가 비싸면 frontier node를 자식노드와 바꾼다.

아까도 얘기했고, 당연한 얘기지만 path-costf를 따지기 때문에 위의 설명에서 c까지의 path-cost보다 b까지의 path-cost가 더 비싸다면, b노드는 무시해도 된다. c까지의 cost가 더 저렴하기 때문이다. 일반적인 경우에, uniform-cost search는 BFS보다 효율적이다.

다음은 BFS이다. frontier중에서 확장된 적이 없는 가장 깊은 노드를 확장하면서 진행한다. tree-search에 기초하고 있고, 그리 크지않은 메모리만 있으면 된다. 또한 무한루프를 피하기 위해서, 새로운 노드가 상위 부모노드중에서 같은것이 있다면 버린다.

위의 그림은 노드들의 탐색하는 과정과, 그에 따른 frontier를 나타낸 것이다. frontier는 stack으로 구현한다. 그리 어렵지 않으므로 frontier node와 비교해가면서 하나씩 살펴보면 된다.

DFS를 평가해 보자. 우선적으로 complete하거나 optimal하지는 않다. m(최고 깊이)이 d(goal의 minimun depth)보다 훨씬 크다면 정말 비효율적인 방법이다. BFS에서 금방 찾을 수 있었을 것이기 때문이다. 유한공한에서는 complete하지만, 불필요한 경로때문에 optimal하지는 않다.
DFS와 동일한 방법이지만 depth에 한계를 두는 depth-limit search라는 것도 있다. 다음 슬라이드를 보자.

이 Depth-limited Search는 limit안에 들어온 경우 complete하게 만들기 위해서 고안한 방법으로, 최대 깊이의 한계를 설정하는 방법이다. 위의 원자핵같은 그림을 보면 중심부에서 외부로 뻗어가는 가지의 바운더리를 설정한 것을 보여준다. 이 limit을 그림에서 보이는 그대로 diameter(지름)이라는 용어로 부른다. 의사코드로 살펴보자.

하지만 이 방법은 전체 공간의 diameter, 다시 말해 전체 공간의 크기를 아는 경우에만 사용할 수 있는 방법이다. 따라서 이 limit을 점근적으로 늘려가며 탐색하는 방법이 있는데 DLS에서 발전한 iterative deepening(lengthening) search이다. 아래의 설명을 참조하자.




iterative-deepening search의 평가내용이다. 점차적으로 limit을 늘려나가는 경우에, complete하고, optimal하다. 이런 점은 breath-first search와 동일하며, 적절한 메모리만 있으면 된다는 점은 depth-first search와 동일하다.

시작점과 도착점에서 동시에 탐색을 진행하는 Bidirectional Search라는 방법도 있다. 항상 사용할 수 있는 방법은 아니지만, BFS의 경우에 깊이가 6이라고 하면, 그 절반인 3만 진행하면 되기 때문에 시간을 많이 줄일 수 있는 방법이다. goal-state가 여러개가 있거나 goal-state에 대한 정확한 state가 아닌 설명만 가능한 경우등 쓸 수 없는 상황이 많은 것이 단점이다.
지금까지의 내용을 두가지 테이블로 비교&정리 하였다. blind(uninformed) search strategy와 tree&graph search 사이의 비교이다. 복잡도는 worst-case의 big-O notation이며, 4가지 기준(Complete, Time, Space, Optimal)으로 나누어졌다.


다음에는 이어지는 학습내용인 2. informed search and exploration,
그리고 추가적으로 n-queens problem을 genetic algorithm으로 해결하는 포스팅을 이어하겠다.
'[ML] > [Lecture]' 카테고리의 다른 글
| [ML/Lecture] 4. Bayesian Networks (0) | 2020.06.20 |
|---|---|
| [ML/Lecture] 3. Uncertainty (0) | 2020.05.04 |
| [ML/Lecture] Assignment #1. solving N-Queens (using genetic -algorithm) report. (0) | 2020.05.03 |
| [ML/Lecture] 2. Informed Search Exploration (0) | 2020.04.08 |
| [ML/Lecture] Intro... (0) | 2020.03.30 |




