
< Learning from Examples (Part B) >

Regression이란 value를 예측하는 것, 즉 그 값을 예상하는 것을 말한다. classification은 분류의 문제, label을 어떻게 붙일것인지를 물어보는 것이였다. 위의 예제처럼 집의 면적이 주어지면, 그 가격을 예측하는 문제가 한가지 예시가 될 수 있다. 이에 연계되어, 그 측정치의 포인트들이 classifier가 될 수도 있다.

모델이 1차식으로 주어지면 위와 같이 h(x) = w1x + w2로 쓸 수 있다. 결국 목표는 예측치와 실제값의 차이가 0이 되도록 하는 것이 목표이다. 각 example들의 차의 제곱을 sum한 것이 squared loss이다.

위 식에서 w1과 w0를 통해 전체 값을 minimize하는 값을 찾고 싶은 것이다. 따라서 미분을 통해 linear regression은 w1과 w0를 찾기가 비교적 쉽다. 따라서 unique한 solution을 구할 수 있다.

그렇지만, 항상 미분으로 값을 계산하기란 쉽지 않다. 특히 linear하지 않은 모델에 대해서는 더 쉽지 않다. 이런 경우에는 gradient-descent search를 통해 minimun 값을 찾게 된다. 현재 w가 있을때, 이 w(weight) 값을 굉장히 조금씩 변화시켜가면서 조정해본다. 이때 loss를 계산할 수 있을 것이다. 이것을 gradient descent search라 한다. 알파는 step-size에 해당한다. 이 크기가 너무 커지게 되면 global-optimal을 뛰어넘을 수도 있고, 너무 작아지게 되면 값을 찾을때까지 시간이 오래 걸리게 될 것이다.

이 gradient descent 방법에는 batch gradient descent와 stochastic gradient descent방법이 있다. batch gradient는 한번 step에서 모든 training data를 사용해서 minimum 값을 찾는 것이다. 따라서 convergence가 느리다. 그래서 각각 다른 데이터로 loop를 돌리고 minimum를 찾고 이를 반복하는 stochastic gradient라는 방법도 있다. 이렇게 하면 빠르기는 하지만 convergence가 보장이 안될수도 있다.


지금까지는 독립변수가 하나 였다면, 이 변수가 여러개가 될 수도 있다. 그렇게 되면 각 attribute에 해당하는 weight값이 필요하게 될 것이다. 이를 multivariate linear regression이라고 한다.

우리가 reqularization을 하는 주된 이유는, 단지 emploss만을 가지고 계산하게 되면 overfitting이 될 수 있었기 때문이였다. linear한 모델에서는 complexity에 해당하는 부분을 regularization하여 패널티를 부여했다. 하지만 linear-regression에서는 w의 절대치가 클수록 complexity가 높다고 생각한다. R1일때와 R2일때를 비교해보면, R1일때는 w1이 0인 지점에서 만나야 하지만, R2일 경우에는 empirial loss가 최소가 되는 w1에서 만날수 있다.
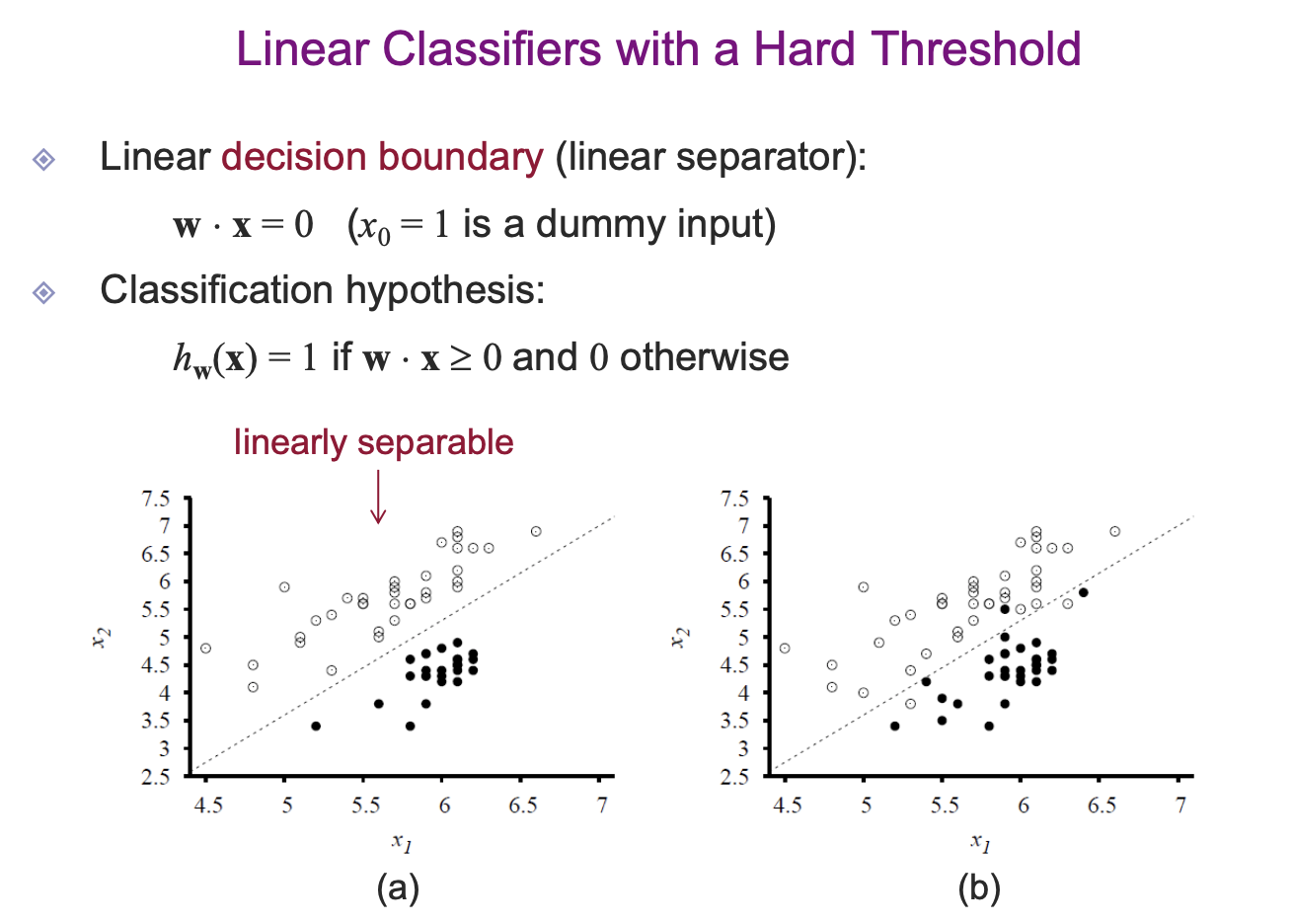
classification하는 데에 쓸 수도 있다.



Hard threshold의 경우처럼 명확하게 딱 구분짓는 것이 쉽지 않을 수도 있다. 따라서 soft한 방식으로 확률같은 형태로 나타내기도 한다. 이는 logistic regression으로, 아웃풋 값이 확률값으로 나오게 된다.


soft, hard 두가지를 비교해서 결과를 보도록 하자.


데이터 인풋이 있다면 이를 layer에 구성하게 된다. activation function에 input을 넣고 그 결과를 output layer에서 본다.



네트워크는 다음과 같이 구성될 수 있다. recurrent neural net 같은 경우는 delay를 가지는 나중에 반영되는 형태가 나올수도 있다.

feed-forward의 예제는 다음과 같다. input으로 들어가는 값이 전개를 통해 다음과 같이 퍼져나가게 된다. 실제로 원래 데이터에서 다양한 functiond을 학습할 수 있다.

가장 기본적인 feed-forward 모델이다. input에서 바로 output이 나오는 것으로, 이런 형태를 single-layer perceptron이라고 한다. input-unit의 한 링크들에는 weight들이 있다. 최적의 parameter를 찾는것이 당연한 목표이다.

이러한 single-layer perceptron들은 이런식의 함수들을 충분히 구현해 낼 수 있다. (다만 exclusive or같은 것은 만들기 힘들다.)

perceptron learning의 핵심은 weight을 조금씩 학습시켜 나가겠다는 의미이며, error를 줄여나가는 방향으로 학습한다. 1/2는 미분에 대한 편의를 위해 집어넣은 값이라고 한다.
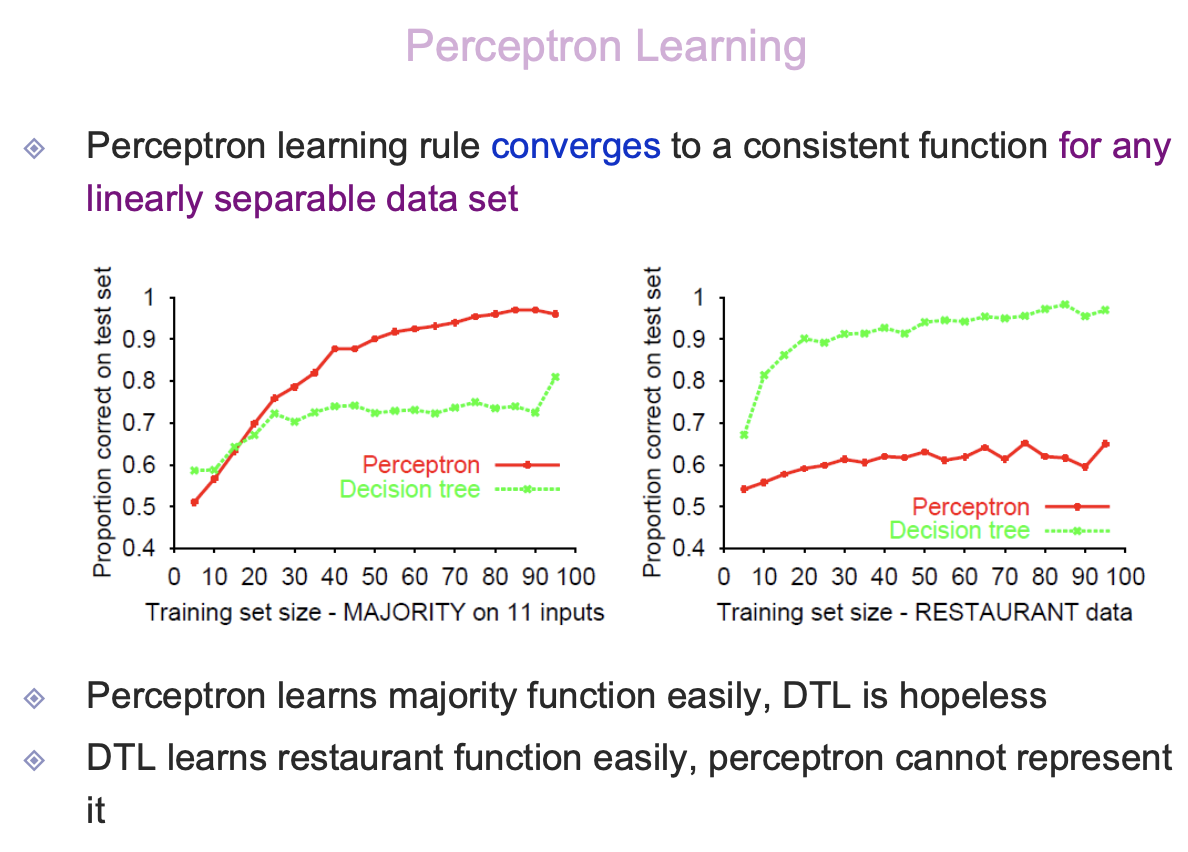
majority-function 같은 경우에는 Perceptron이 잘 배우게 된다. (decision-tree같은 경우는 잘 학습하지 못한다) 손님이 얼마나 올 것인가와 같은 restaurant-function같은 경우에는 잘 동작하지만, perceptron의 경우는 잘 동작하지 않는다.

이 layer가 꼭 한개일 필요는 없다. layer를 늘리고 가중치를 부여할수록 hidden layer를 만들 수 있다.

두개의 다른 opposite-facing function을 combine하게 되면 다음과 같은 ridge형태를 띄게 된다. 이를 또 두개를 조합하면 bump형태를 띄게 된다. 또한 한 layer를 추가하였을때, 몇개의 hidden unit을 주는지는 시도를 해보는 수 밖에 없다.

기본적으로 error를 minimize하고 싶은 것인데, gradient가 0으로 가까이 가게끔 하고 싶은 것이다. 알파는 learning weight이다. weight를 update할 때, 우선은 input값이 주어지면 임의의 weight을 assign을 하고 계산을 하게 된다. 그렇게 하면 hidden layer등 학습이 되게 되고, 최종 값이 나오게 된다. 이때, 실제 아웃풋 값을 이용하게 되면, gradient가 0이 되는 방향으로 거꾸로 계산할 수 있게 된다.



이를 back-propagation-learning이라고 한다. weight을 update하는 진행방향이 output->input으로 진행한다. 위의 경우에는 trainning data에 대해서 weight들이 어떻게 학습되어가고 있는지를 보게되면, convegence가 느리고, local minimun에 빠질 가능성 또한 존재한다. (추후에 관련 내용들을 보완해야 겠다.)

hidden-layer가 꼭 하나일 필요는 없다. restaurant data에 대해서는 decision-tree가 좀 더 좋은 성능을 보여주고 있다. pattern을 인식하는 task에서는 꽤 잘 동작한다는 것을 보여주고 있다. 직관적으로 이해하는 데에는 조금 어려움이 존재한다.
'[ML] > [Lecture]' 카테고리의 다른 글
| [ML/Lecture] 8. Introduction to Deep Learning (0) | 2020.06.30 |
|---|---|
| [ML/Lecture] 6. Learning from Examples (Part A) (0) | 2020.06.25 |
| [ML/Lecture] 5. Inference in BN (0) | 2020.06.20 |
| [ML/Lecture] 4. Bayesian Networks (0) | 2020.06.20 |
| [ML/Lecture] 3. Uncertainty (0) | 2020.05.04 |




