다익스트라(Dijkstra) 알고리즘은 하나의 시작 정점에서 끝 정점까지의 최단경로를 구하기 위한 알고리즘이다.
음의 가중치를 가지지 않으며, PriorityQueue의 사용여부에 따라 시간복잡도는 O(V^2)~O(E+VlogV)까지 나타난다.
음의 가중치를 허용하는 경우에는 벨판-포드(Bellman-Ford)알고리즘을 사용할 수 있다. (모든 정점들에 대한 최단경로를 구하는 데는 DP개념을 적용한 플로이드-워샬(Floyd-Warshall)을 사용할 수 있다.)
본론으로 돌아와서, 시작 정점이 주어졌을 때 각 정점까지의 최단경로를 구하려면 어떻게하면 될까?
다음 코드는 priorityQueue를 사용하지 않는 코드이다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class DijkstraTest {
public static void main(String[] args) throws NumberFormatException, IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int V = Integer.parseInt(br.readLine());
int start=0; // 출발점
int end = V-1; // 도착점
int[][] adjMatrix = new int[V][V];
StringTokenizer st = null;
for(int i=0; i<V; i++) {
st = new StringTokenizer(br.readLine());
for(int j=0; j<V; j++) {
adjMatrix[i][j] = Integer.parseInt(st.nextToken());
}
}
int[] distance = new int[V];
boolean[] visited = new boolean[V];
Arrays.fill(distance, Integer.MAX_VALUE);
distance[start]=0;
for(int i=0; i<V; i++) {
int min = Integer.MAX_VALUE;
int current = 0;
// step1. 처리하지 않은 정점들 중에 출발지에서 가장 가까운(최소비용) 정점 선택
for(int j=0; j<V; j++){
if(!visited[j] && min>distance[j]) {
min = distance[j];
current = j;
}
}
visited[current] = true;
if(current == end ) break;
// step2. 선택된 current를 경유지로 하여 아직 처리하지 않은 다른 정점으로의 최소비용 따져본다.
for(int j=0; j<V; j++) {
if(!visited[j] && adjMatrix[current][j] != 0 && distance[j] > min + adjMatrix[current][j]) {
distance[j] = min + adjMatrix[current][j];
}
}
}
System.out.println(distance[end]);
}
}하나씩 분석해 보도록 하자.
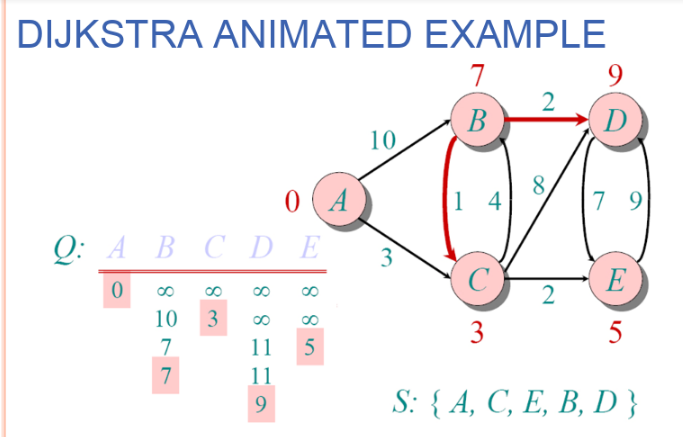
1. 먼저 인접리스트를 생성하고, 각 정점까지의 최소거리를 담을 distance배열과, 방문여부를 체크할 visited 배열을 만든다. 그리고 distance배열의 초기화는 INF로 한 뒤, start의 인덱스는 0으로 설정해 준다. 시작정점->시작정점의 거리는 당연히 0이기 때문이다.
for(int i=0; i<V; i++) {
st = new StringTokenizer(br.readLine());
for(int j=0; j<V; j++) {
adjMatrix[i][j] = Integer.parseInt(st.nextToken());
}
}
int[] distance = new int[V];
boolean[] visited = new boolean[V];
Arrays.fill(distance, Integer.MAX_VALUE);
distance[start]=0;2. 다음은 정점 수만큼 돌면서 수행하는 작업내용이다(i for문 내부).
1단계는 처리하지 않은 정점들 중에 출발지에서 가장 가까운 정점을 선택한다. 그 정점의 비용, 정점번호를 각각 min과 current에 저장한다.
// step1. 처리하지 않은 정점들 중에 출발지에서 가장 가까운(최소비용) 정점 선택
for(int j=0; j<V; j++){
if(!visited[j] && min>distance[j]) {
min = distance[j];
current = j;
}
}3. 해당 정점을 방문처리한다.
visited[current] = true;4. 마지막으로 선택한 지점을 경유지로 하여, 아직 방문하지 않은 각 정점까지의 최소비용을 따져본다.
즉, 아직 방문하지 않았고, 현재 지점에서 그 정점까지의 길이 있으면서,
시작점 -> 그 정점까지의 거리 >>> 시작점->현재점까지 거리 + 현재점->그정점까지의 거리 를 비교해서 작은값으로 갱신한다!
// step2. 선택된 current를 경유지로 하여 아직 처리하지 않은 다른 정점으로의 최소비용 따져본다.
for(int j=0; j<V; j++) {
if(!visited[j] && adjMatrix[current][j] != 0 && distance[j] > min + adjMatrix[current][j]) {
distance[j] = min + adjMatrix[current][j];
}
}그러면 결과가 어떻게 될까?
먼저 첫 루프를 도는 상황에서 current, 즉 출발점에서 가장 가까운(가까웠던) 점은 방문처리가 되었을 것이다. 이 current는 곧 경유지가 된다. 그리고 나서, 시작점에서 바로 각 정점까지 가는 거리와, 경유지를 거쳐 가는 거리를 비교해서 경유지를 거쳐 가는 방법이 작다면, 그 값으로 전부 갱신이 되었을 것이다. 다익스트라를 구현하는 방법은 여러가지가 있는데, 이 방법처럼 distance배열을 유지하게 되면, 시작점에서 current까지의 거리는 INF가 아니라면, 루프가 끝난 시점에 항상 최소값을 보장한다. 따라서 current가 end값이 나온다면, 해당 값을 출력하면 된다!
<PriorityQueue를 이용한 Dijkstra구현>
import java.util.*;
class Element implements Comparable<Element>{
int idx;
int distance;
Element(int idx, int distance){
this.idx = idx;
this.distance = distance;
}
@Override
public int compareTo(Element o) {
return this.distance - o.distance;
}
}
public class test {
static boolean[] visit;
static int[] dist;
static int[][] ad;
static int v, e;
static final int inf = 100000;
public static void dijkstra(int start){
PriorityQueue<Element> que = new PriorityQueue<>();
dist[start] = 0;
que.offer(new Element(start, dist[start]));
while(!que.isEmpty()){
Element tmp = que.poll();
int distance = tmp.distance;
int idx = tmp.idx;
if(distance > dist[idx])
continue;
for(int i = 1; i <= v; i++){
if(ad[idx][i] != 0 && dist[i] > dist[idx] + ad[idx][i]){
dist[i] = dist[idx] + ad[idx][i];
que.add(new Element(i, dist[i]));
}
}
}
System.out.println();
for(int i =1 ; i <= v; i++){
System.out.print(dist[i]+" ");
}
}
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
v = sc.nextInt();
e = sc.nextInt();
visit = new boolean[v+1];
dist = new int[v+1];
ad = new int[v+1][v+1];
for(int i = 0; i <= v; i++){
dist[i] = inf;
}
for(int i = 0; i < e; i++){
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
ad[a][b] = c;
ad[b][a] = c;
}
dijkstra(1);
}
}
'[Algorithms] > [Theory]' 카테고리의 다른 글
| [Theory] Graph 5. MST - PRIM (0) | 2021.03.23 |
|---|---|
| [Theory] Graph 4. MST - KRUSKAL (0) | 2021.03.22 |
| [Theory] Graph 3. 서로소 집합(Disjoint-set) aka, Union-Find (0) | 2021.03.18 |
| [Theory] Graph 2. 인접 리스트(Adjacent List) 탐색 (0) | 2021.03.18 |
| [Theory] Graph 1. 인접 행렬(Adjacent Matrix) 탐색 (0) | 2021.03.17 |




