728x90
그래프가 주어졌을때, 이를 표현하는 방법은 여러가지가 있다. 정점을 중심으로 구분하는 경우, 대표적으로 인접 행렬과, 인접 리스트 방식이 있고, 간선을 중심으로 표현하는 간선 리스트 방식이 있다. 그 중에서 인접 행렬(Adjacent Matrix)로 표현하는 방법을 간단히 정리한다.
인접 행렬(Adjacent Matrix)에서 인접( Adjacency)의 의미는,
"두개의 정점(Vertex)에 간선(Edge)이 존재하면 서로 인접" 하다고 한다.
따라서 인접 행렬(Adjacent Matrix)의 구현은, VxV크기의 2차원 배열을 이용해서 간선의 정보를 저장한다.
예시) 다음과 같은 그래프가 주어졌다고 하자.

이 그래프를 Matrix상에 표현하면 아래와 같다. 간선들 사이에 방향이 없으므로, [From -> To] 와 [To -> From] 을 모두 나타내였다.
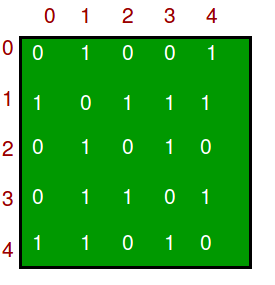
이와 같이 인접 행렬(Adjacent Matrix) 로 그래프를 나타내게 되면, 별도의 자료구조를 구현할 필요 없이 단순 배열로 문제를 해결할 수 있으므로 구현이 쉬워진다. 하지만 완전그래프가 아닌 이상, 배열 사이사이 쓸모없는 정보인 0이 들어가게 된다. 즉, 연결되지 않은 점들사이의 정보도 포함되는 것이다. 이는 그래프가 희소그래프(Sparse Graph)에 가까워질수록 문제가 더 심각해 진다. 이 문제를 연결리스트로 해결한 방법이 인접 리스트(Adjacent List)이다.
일단 먼저 인접 행렬(Adjacent Matrix) 의 코드를 살펴보면 다음과 같다.
- 데이터 인풋
for(int i=0; i<C; i++) {
st = new StringTokenizer(in.readLine(), " ");
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
adjMatrix[to][from] = adjMatrix[from][to] = true; // 해당 예제는 무향그래프이므로
}
- 단순 BFS 구현
private static void bfs() {
Queue<Integer> queue = new LinkedList<Integer>();
boolean[] visited = new boolean[N];
// 탐색 시작 정점: 0으로 출발
int start = 0;
queue.offer(start);
visited[start] = true;
while(!queue.isEmpty()) {
int current = queue.poll();
// 현재 정점에 관련된 처리
System.out.println((char)(current+65));
// 인접 정점 탐색
for(int i=0; i<N; i++) {
if(adjMatrix[current][i] // 인접 정점
&& !visited[i]) { // 미방문 정점
queue.offer(i);
visited[i]=true;
}
}
}
}
- 전체 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
//그래프 데이터
public class adjMatrix {
static int N;
static boolean[][] adjMatrix;
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(in.readLine());
int C = Integer.parseInt(in.readLine());
adjMatrix = new boolean[N][N];
StringTokenizer st = null;
for(int i=0; i<C; i++) {
st = new StringTokenizer(in.readLine(), " ");
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
adjMatrix[to][from] = adjMatrix[from][to] = true;
}
bfs();
}
private static void bfs() {
Queue<Integer> queue = new LinkedList<Integer>();
boolean[] visited = new boolean[N];
// 탐색 시작 정점: 0으로 출발
int start = 0;
queue.offer(start);
visited[start] = true;
while(!queue.isEmpty()) {
int current = queue.poll();
// 현재 정점에 관련된 처리
System.out.println((char)(current+65));
// 인접 정점 탐색
for(int i=0; i<N; i++) {
if(adjMatrix[current][i] // 인접 정점
&& !visited[i]) { // 미방문 정점
queue.offer(i);
visited[i]=true;
}
}
}
}
}
728x90
'[Algorithms] > [Theory]' 카테고리의 다른 글
| [Theory] Graph 6. 최소비용 - 다익스트라(Dijkstra) 알고리즘 (0) | 2021.04.01 |
|---|---|
| [Theory] Graph 5. MST - PRIM (0) | 2021.03.23 |
| [Theory] Graph 4. MST - KRUSKAL (0) | 2021.03.22 |
| [Theory] Graph 3. 서로소 집합(Disjoint-set) aka, Union-Find (0) | 2021.03.18 |
| [Theory] Graph 2. 인접 리스트(Adjacent List) 탐색 (0) | 2021.03.18 |




